三角形中与垂心有关的等量关系的证明
三角形的三条高线所在直线的交点称为三角形的垂心。充分利用垂心性质可以帮助我们解决一些初中几何问题,现举例说明如下。
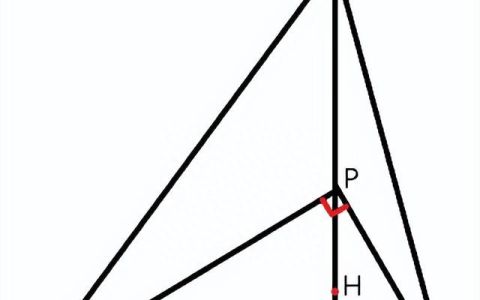
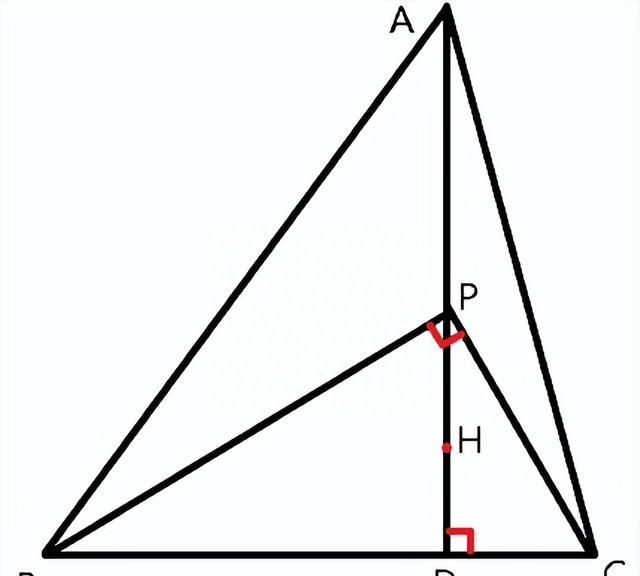
题目1:如图1,在锐角△ABC中,AD⊥BC于D,H为垂心,在AD上有一点P,且∠BPC=90°。
求证PD²=AD·HD。
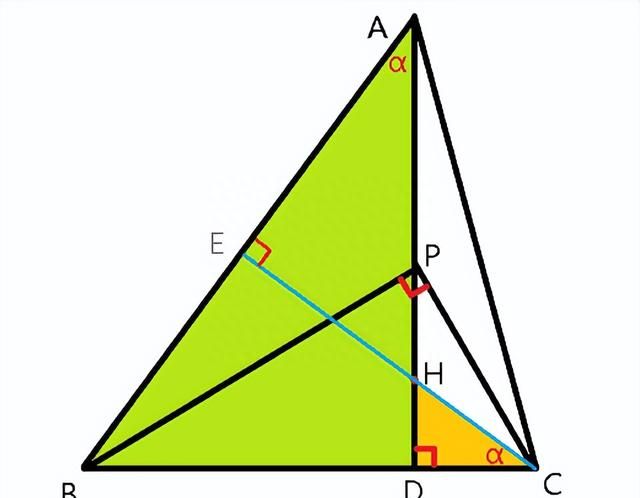
解题思路:采用逆推法思考:本题欲求PD²=AD·HD,我们知道,根据直角三角形射影定理公式,PD²=BD·DC,想办法证明AD·HD= BD·DC就行了。连接CH并延长交AB于E(图2),使得AD·HD= BD·DC中的四条线段包含在RT△ABD和RT△CHD中。
易证Rt△ABD∽RT△CHD,
AD/BD=DC/HD,
AD·HD= BD·DC,
PD²=AD·HD成立。
题目2:如图1,在三角形ABC中,AD是BC边上的高,BE是AC边上的高,AD=BD,H为垂心。求证DH=DC。
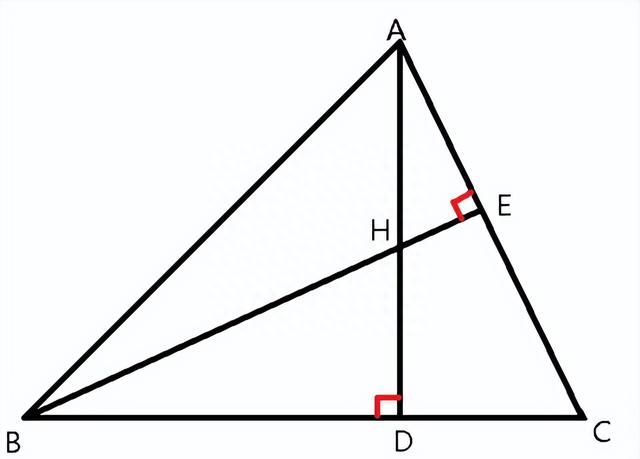
解题思路:
①在Rt△BDH和Rt△ADC中,AD=BD,∠CBE=∠CAD,故Rt△BDH≌ Rt△ADC,DH=DC成立。
②另一种解题方法是利用隐圆解题,如图2,易证A、B、D、E和H、D、C、E四点共圆,得知Rt△HDC为等腰三角形,所以DH=DC。
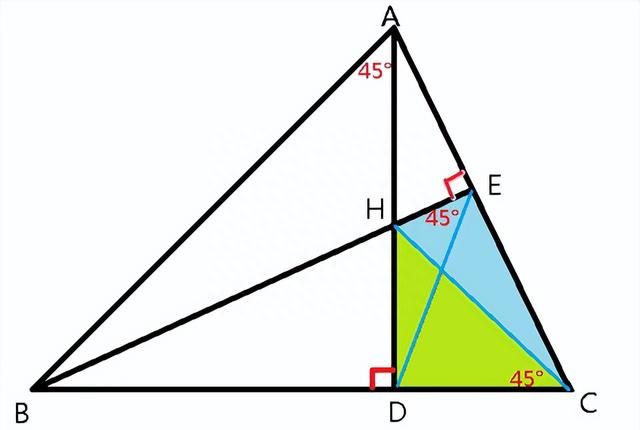
③利用垂心性质(图3),已知Rt△ADB为等腰三角形,∠ABC=45°。H为垂心,连接CH并延长交AB于F,则CF⊥AB,Rt△BFC亦为等腰直角三角形,也即Rt△HDC为等腰三角形,所以DH=DC。
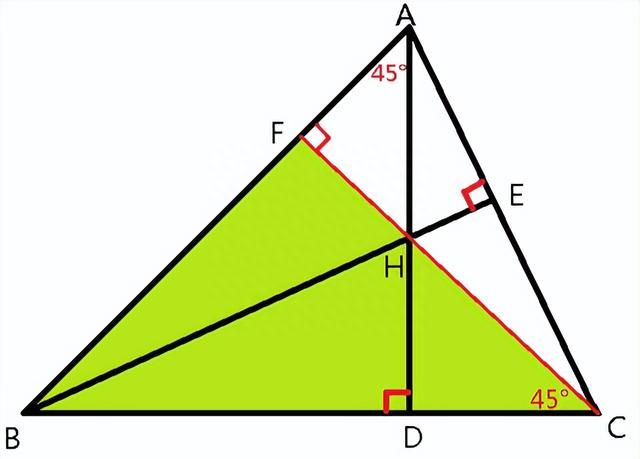
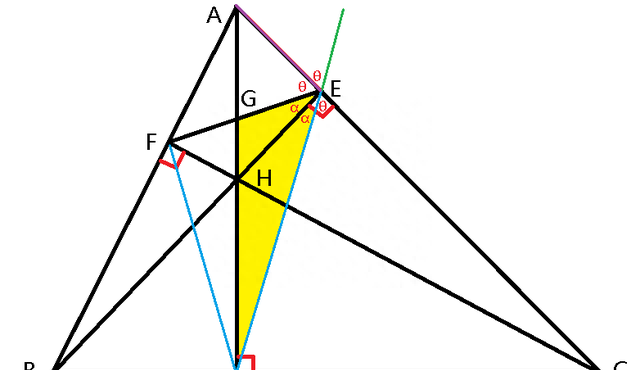
题目3:如图1,在△ABC中,AD、BE、CF是高,H为垂心,EF交AD于G。求证GH/DH=GA/DA。
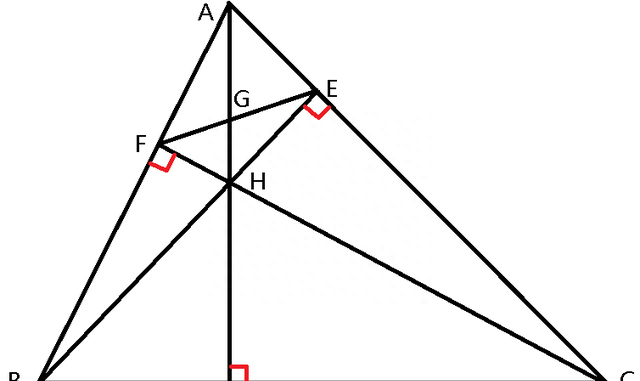
解题思路:根据题意,连接DF、DE,点H是△EFD的内心(锐角三角形的垂心H必为其垂足三角形的内心,详见三角形的四心及经典例题3例),EH为△EGD的∠GED的角平分线,∠GEH=∠DEH(图2)。根据三角形内角平分线定理有:
EG/ED=GH/DH。
又易证AE为△EGD的外角平分线,根据三角形外角平分线定理(详见三角形内角和外角平分线定理及其应用):
EG/ED= GA/DA,
故GH/DH=GA/DA成立。
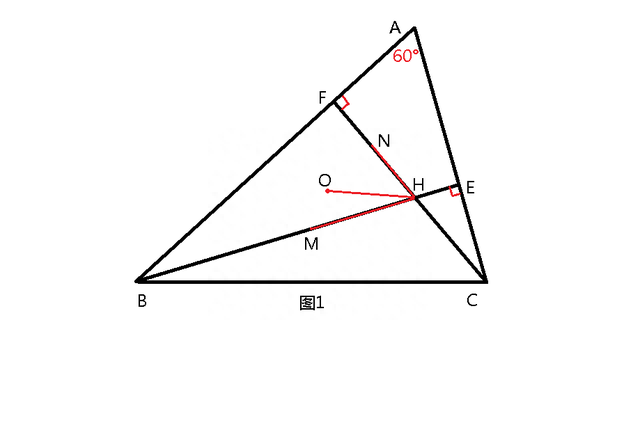
题目4:如图1,在△ABC中,∠A=60°,AB>AC,点O是外心,两条高BE、CF交于H点,点M、N分别在线段BH、HF上,且满足BM=CN。证明MH+NH=√3 HO。
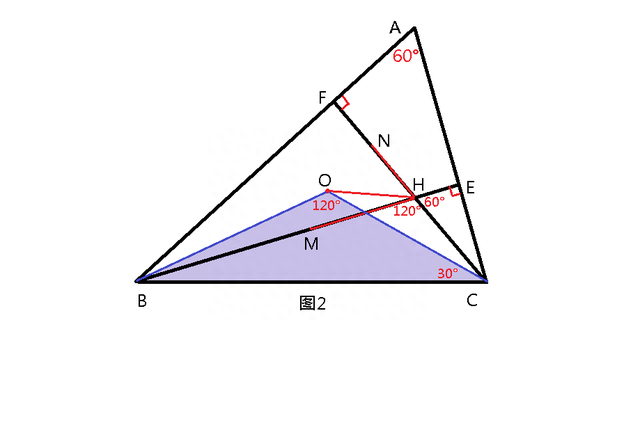
解题思路:已知∠A=60°,点O是外心,即为△ABC外接圆的圆心,连接OB、OC,则△OBC为顶角为120°的等腰三角形(图2,圆心角为圆周角的2倍),OB、OC、BC边长比关系1∶1∶√3。
图中易证∠BOC=∠BHC=120°,故B、C、H、O四点共圆。
根据托勒密定理得:
HO·BC+HC·OB=HB·OC,即:
√3 OB·HO+HC·OB=HB·OB,简化为:
√3 HO+HC =HB,变形为:
√3 HO+(CN-NH) =BM+MH。
已知BM=CN,上式进一步简化为:
√3 HO=MH+NH,
故MH+NH =√3 HO成立。
该题相关内容详见托勒密定理结合三角形的边长比例关系解题中的题目7。